Problems with products? Control strategies for models with interaction and quadratic effects
Abstract
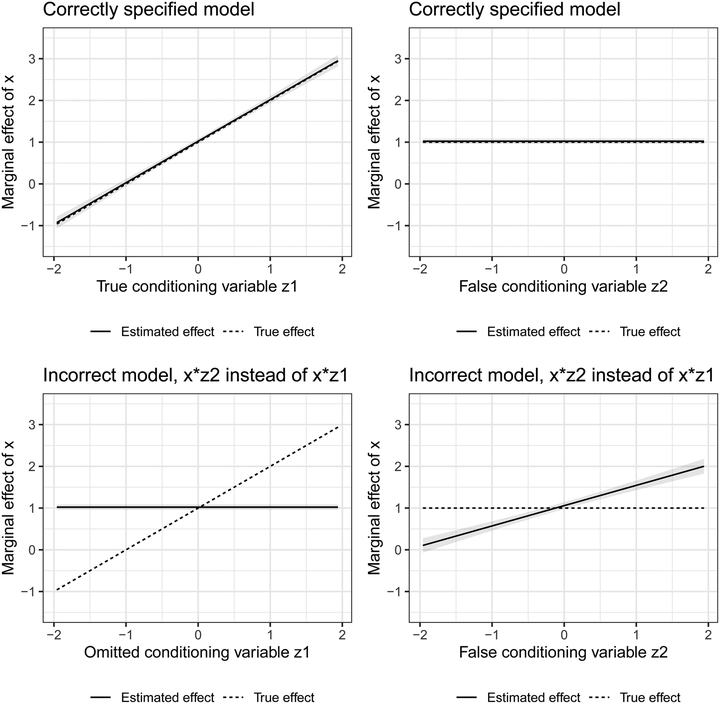
Models testing interactive and quadratic hypotheses are common in Political Science but control strategies for these models have received little attention. Common practice is to simply include additive control variables, without relevant product terms, into models with interaction or quadratic terms. In this paper, we show in Monte Carlos that interaction terms can absorb the effects of other un-modeled interaction and non-linear effects and analogously, that included quadratic terms can reflect omitted interactions and non-linearities. This problem even occurs when included and omitted product terms do not share any constitutive terms. We show with Monte Carlo experiments that regularized estimators, the adaptive Lasso, Kernel Regularized Least Squares (KRLS), and Bayesian Additive Regression Trees (BART) can prevent the misattribution of interactive/quadratic effects, minimize the problems of efficiency loss and overfitting, and have low false-positive rates. We illustrate how inferences drawn can change when relevant product terms are used in the control strategy using a recent paper. Implementing the recommendations of this paper would increase the reliability of conditional and non-linear relationships estimated in many papers in the literature.